Polymers: Equilibrium and Non-equilibrium Statistical Mechanics

A large part of our work on this topic can be classified as Biophysical Chemistry.

I. Biophysical Chemistry

Adsorption on a spherical vesicle (see publication 1)

We have studied the free energy for translocation of a polymer from the outside of a spherical vesicle to the inside. The process is assumed to be driven by the adsorption of the polymer on the inner surface of the vesicle. Partition functions for chains adsorbed on the inside and outside have been calculated. We argue that in the case where the polymer is adsorbed on the outer surface too, the entropic barrier for translocation is absent - thus weak adsorption on the outer surface facilitates translocation to the inside. We analyze the adsorption energy and find the free energy profile for the process. We argue that the motion corresponds to a polymer crossing a region with a change in free energy per segment. Based upon our analysis of the behaviour of kinks in such a problem (see below), we conclude that the translocation can occur with a crossing time proportional to the length of the chain.

For earlier work on adsorption and polymer models, see publications 5-9

Kramers Problem for Long Chain Molecules (see publications 2-4)

Polymer Crossing a Barrier

We have recently proposed a kink mechanism for the escape of a polymer over a barrier. The motion of the polymer was modelled by the Rouse model. The inclusion of the barrier leads to a non-linear Rouse model. The crossing the barrier can take place by end-crossing over hairpin crossing. Once a portion has crossed, further crossing occurs by kink motion. The kink is just a special soliton like solution of the non-linear Rouse model. The motion of the kink leads to a crossing time proportional to the length L of the polymer, if there is a free energy gain in crossing the barrier. Otherwise, the time scales as L²

Hairpin Crossing

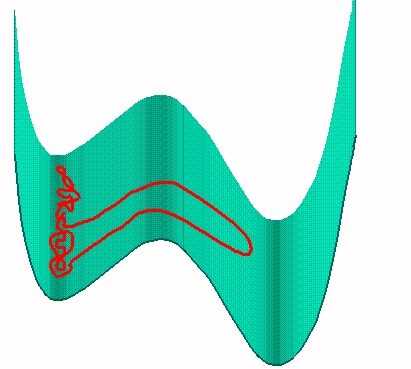
The figure shows the formation of a hairpin in the crossing. The activation energy for the hairpin is independent of the length of the chain. It is equal to two times the activation energy for the end crossing. As the hair pin can be formed anywhere in the chain, the probability of formation is proportional to the length of the chain.

End Crossing

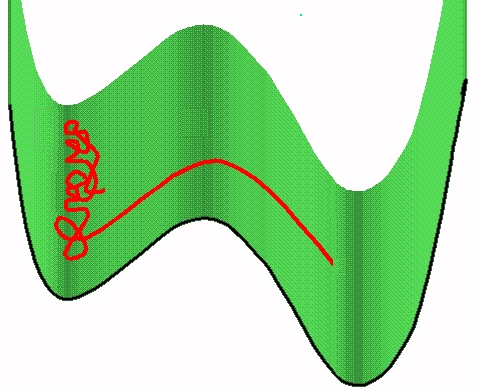
The figure shows end-crossing. This can occur only at the two ends.

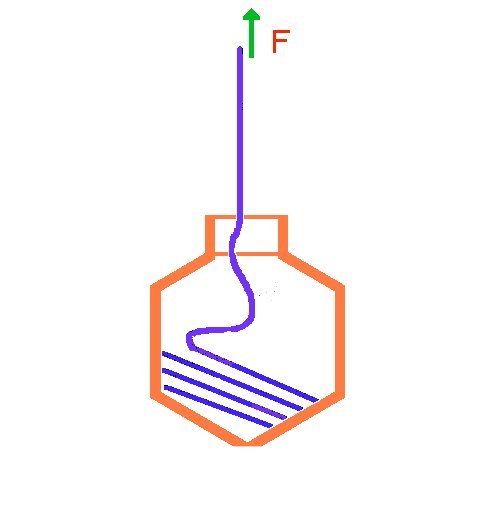
Pulling a Polymer out of a well

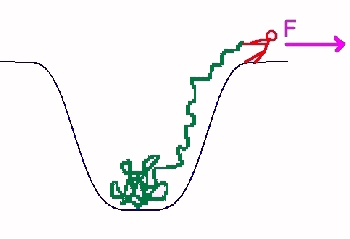
Recently there have been experiments in which the two strands of a DNA were mechanically separated by the application of forces on the two strands. As a model for the dynamics of this process, we have investigated the dynamics of a polymer, initially trapped in a potential well, subjected to a force at one of its ends, trying to pull it out (see figure). We find that if the force F is below a critical value F_c, the process is activated and the activation energy is proportional to the length of the chain. If the force is above F_c, then the process is not activated and will occur spontaneously. We use the Rouse model to analyse the dynamics in this case. We argue that the mean segment position obeys a moving boundary value problem, which we solve exactly, to find that the time required to pull out a chain of length L scales like L². (see publication 7)

Breaking of a Polymer

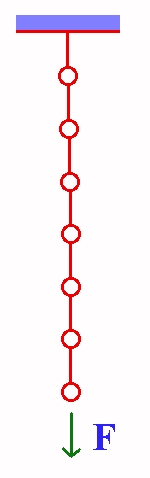
A polymer molecule which is fixed at one end and is acted upon by a force at the other. How to describe the dynamics of the breaking? The polymer is assumed to be a linear chain connected together by bonds which satisfy the Morse potential. The applied force is found to modify the Morse potential so that the minimum is now metastable. Breaking is just the decay of this metastable bond, by going over the barrier. Increasing the force causes the potential to get more and more distorted and eventually to the disappearance of the barrier. The rate of breaking was first calculated using multidimensional quantum transition state theory under the harmonic approximation. It is then possible to analytical exprssion for the rate of breaking. We have calculated the rate of breaking for a model, which mimics polyethylene. Under the harmonic approximation, many body effects are found to lower this rate by at the most one order of magnitude. Quantum effects are found to increase the rate of breaking. They are significant at temperatures less than 150 K. At 300 K, the calculations predict a bond in polyethylene to have a lifetime of only seconds at a force which is only half the limiting force. Calculations were also done using the Lennard-Jones potential. Comparison of the classical results with the simulations of Oliveira and Taylor (J. Chem. Phys. 101, 10118 (1994)) showed our results to be two to three orders of magnitude higher. As a possible explanation of discrepancy, we consider the translational motion of the broken chains. Using a continuum approximation for the chain, we find that in the absence of friction, the rate of the process can be limited by the rate at which the two broken ends separate from one another and the lowering of the rate is utmost an order of magnitude (for polyethylene). Oliveira and Taylor consider the motion of the atoms to be damped. In such cases, for the parameters that they take, we found that the rate can be lowered by two to three orders of magnitude, in agreement with their simulation.

Forcing a Polymer out of a potential well

We consider the forced escape of a polymer out of a potential well by the application of an external field. The process has two steps - crossing the activation barrier, and translocation of the long chain over the barrier. We have suggested that this occurs by the motion of a kink, whose shape and velocity change as more and more beads of the polymer come out of the potential well. We find that for a polymer which is not very long, this mechanism leads to a translocation time is t_{trans} ~ ln (N), where N is the number of beads in the polymer chain. For very long chains, the time become proportional to N (see publication 13).

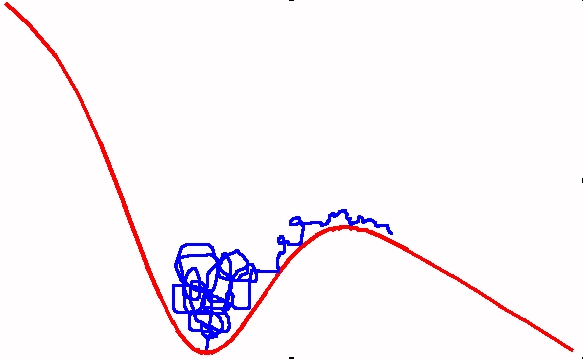
Effect of Pulling on DNA packaging into a Viral Capsid

How does a viral DNA get packaged into its capsid? There is a molecular machine at is head, driven by ATP hydrolysis, that does the packing. Recently there have been a single molecule experiment in which the packaging of the DNA into the viral capsid has been studied. A DNA molecule while in the process of going into the capsid, was pulled at the free end with a force F (poor DNA!) (see Smith et. al. Nature, 413, 748 2002). The rate of packing was measured as a function of F (see figure). We have suggested an equation for the rate of packing as a function of the pulling force. Interestingly, the equation is very similar to the Butler-Volmer equation!

For more information, please see the listed publications below

K. Kiran Kumar and K. L. Sebastian: Adsorption assisted translocation of a polymer in to a spherical vesicle. Physical Review E, 62, No. 5 (2000). See cond-mat/9908426.
K. L. Sebastian: Kink Motion in the Barrier Crossing of a Chain molecule. Physical Review E, 61, 3245 (2000). An early version available as: cond-mat/9907003.
K. L. Sebastian: Kink motion in a chain molecule driven through a pore. to appear in J. Am. Chem. Soc., 122, 2972 (2000).
K. L. Sebastian and A. K. R. Paul: Barrier crossing of a long chain molecule - the kink mechanism. to appear in Physical Review E, (2000). available as cond-mat/0001043.
K. L. Sebastian and Rosabella Puthur: Multidimensional transition state theory and beyond for the breaking of a polymer. Chemical Physics Letters, 304, 399 (1999).
Rosabella Puthur and K. L. Sebastian: The Rate of Breaking of a Polymer under mechanical stress. to be submitted (2000).
K. L. Sebastian: Pulling a polymer out of a potential well and the mechanical unzipping of DNA. to appear in Physical Review E, (2000).
N. Chakravarti and K. L. Sebastian: Fractional Brownian Motion Model for polymers. Chemical Physics Letters, 267, 9 (1997).
K. L. Sebastian: Path Integrals for fractional Brownian motion. Journal of Physics A., 28, 4305 (1995).
K. Sumithra and K. L. Sebastian: Polymers at chemically random surfaces. Journal of Physical Chemistry, 98, 9312 (1995).
K. L. Sebastian and K. Sumithra: Adsorption of a polymer on a random surface. Physical Review E, 47, R32, (1993).
K. L. Sebastian: Statistical Thermodynamics of the peeling of a polymer from a line. Chemical Physics Letters, 194, 375 (1992).
Keshav Kumar and K. L. Sebastian: Forcing a polymer out of a potential well. to appear in Chemical Physics Letters (2002).
K. P. Santo and K. L. Sebastian: Simple mode for the kinetics of packaging of DNA into a capsid against an external force. Physical Review E, 65 (2002).

back to main page